Gebrochenrationale Funktionen

Bei gebrochen rationalen Funktionen handelt es sich um Brüche von Polynomfunktionen. Schau dir an, wie man Definitionslücken identifiziert und Asymptoten bestimmt. Lies weiter und erfahre mehr dazu!

Übungen
starten

Arbeitsblätter
anzeigen

Lehrer*innen
fragen

Inhaltsverzeichnis zum Thema Gebrochenrationale Funktionen

Was sind gebrochen rationale Funktionen?
- Echt gebrochen rationale Funktion vs. unecht gebrochen rationale Funktion
Eigenschaften gebrochen rationaler Funktionen
- Definitionslücken und Polstellen
- Asymptoten gebrochen rationaler Funktionen
Kurvendiskussion gebrochen rationaler Funktionen
Aufgaben zu gebrochen rationalen Funktionen
Ausblick – das lernst du nach gebrochen rationalen Funktionen
Zusammenfassung zum Thema Gebrochen rationale Funktionen
Häufig gestellte Fragen zum Thema Gebrochen rationale Funktionen

Du willst ganz einfach ein neues Thema lernen
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?

5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.

92%

der Schüler*innen hilft sofatutor beim selbstständigen Lernen.
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.

93%

der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert.
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.

94%

der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.

Noch nicht angemeldet? 30 Tage kostenlos testen

Lerntext zum Thema Gebrochenrationale Funktionen

Was sind gebrochen rationale Funktionen?

Eine gebrochen rationale Funktion ist eine Funktion, die durch einen Bruch zweier Polynomfunktionen beschrieben wird. Allgemein hat eine gebrochen rationale Funktion $f(x)$ die Form:

$$f(x) = \frac{p(x)}{q(x)}$$

Dabei sind $p(x)$ und $q(x)$ Polynomfunktionen der Form $a_n x^n + a_{n-1} x^{n-1} + \dots + a_1 x + a_0$ und es gilt $q(x) \neq 0$.

Echt gebrochen rationale Funktion vs. unecht gebrochen rationale Funktion

Man unterscheidet zwei Arten von gebrochen rationalen Funktionen:

Eine echt gebrochen rationale Funktion liegt vor, wenn der Grad (die höchste $x$-Potenz) des Zählerpolynoms kleiner ist als der Grad des Nennerpolynoms.

Beispiel:
$$f(x) = \frac{x + 3}{x^2 - 4}$$

Eine unecht gebrochen rationale Funktion hat ein Zählerpolynom, dessen Grad mindestens genauso groß wie der des Nennerpolynoms ist.

Beispiel:
$$f(x) = \frac{x^2 + 1}{x - 2}$$

Eine unecht gebrochen rationale Funktion lässt sich durch Polynomdivision in eine Funktion mit ganzrationalem und echt gebrochen rationalem Anteil zerlegen.

Eigenschaften gebrochen rationaler Funktionen

Gebrochen rationale Funktionen haben besondere Merkmale, die bei der Analyse der Funktionskurven eine wichtige Rolle spielen:

Definitionslücken und Polstellen

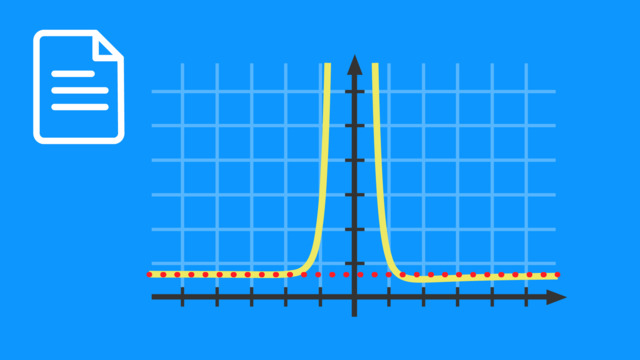
Eine gebrochen rationale Funktion ist an den Stellen nicht definiert, an denen der Nenner $q(x)$ gleich null ist (also an den Nullstellen der Polynomfunktion im Nenner). Solche Stellen heißen Definitionslücken. Ist die Definitionslücke nicht durch Kürzen des Funktionsterms zu beseitigen, spricht man von einer Polstelle.

Asymptoten gebrochen rationaler Funktionen

Ein wichtiges Merkmal gebrochen rationaler Funktionen sind die sogenannten Asymptoten. Diese sind Geraden, denen sich der Graph der Funktion immer weiter annähert, ohne sie zu erreichen.

Es gibt:

senkrechte Asymptoten an Polstellen,
waagerechte Asymptoten, wenn der Grad des Zählers kleiner oder gleich dem des Nenners ist,
schräge Asymptoten, wenn der Grad des Zählers genau um $1$ größer ist als der des Nenners.

Beispiele:

Die gebrochen rationale Funktion $f(x)=\dfrac{x^2-3}{4x}$ hat eine senkrechte Asymptote bei $x=0$ und eine schräge Asymptote bei $y=\dfrac{1}{4}x$.

Hyperbel mit schräger Asymptote

Die gebrochen rationale Funktion $g(x)=\dfrac{x^2+2}{x^3}+1$ hat eine senkrechte Asymptote bei $x=0$ und eine waagerechte Asymptote bei $y=1$.

Hyperbel mit waagerechter Asymptote

Asymptoten verhalten sich ähnlich wie eine „magnetische“ Grenze, die von der Kurve nicht überschritten wird, egal wie nah sie ihr kommt.

Kurvendiskussion gebrochen rationaler Funktionen

Die Kurvendiskussion gebrochen rationaler Funktionen beinhaltet typischerweise folgende Schritte:

Definitionsbereich bestimmen: alle Werte von $x$, für die der Nenner nicht null wird
Nullstellen berechnen: Zähler gleich null setzen und lösen
Polstellen und Definitionslücken bestimmen: Nenner gleich null setzen und überprüfen, ob der Funktionsterm kürzbar ist
Asymptoten bestimmen: horizontale, vertikale oder schräge Asymptoten
Extrempunkte und Wendepunkte berechnen: Ableitungen bestimmen, um lokale Hoch-, Tiefpunkte und Wendepunkte zu finden

Ein weiteres, typisches Aufgabenformat ist die Rekonstruktion von gebrochen rationalen Funktionen.

Aufgaben zu gebrochen rationalen Funktionen

Berechne die Definitionslücke von $f(x)=\frac{x-5}{x^2-25}$.

Welche Art von Asymptoten hat $f(x)=\frac{2x^2}{x^2+1}$?

Bestimme die Nullstelle der Funktion $f(x)=\frac{x-1}{x+2}$.

Ausblick – das lernst du nach gebrochen rationalen Funktionen

Als Nächstes kannst du dein Wissen über die Ableitungen vertiefen, um weitere Funktionsanalysen durchzuführen.

Zusammenfassung zum Thema Gebrochen rationale Funktionen

Gebrochen rationale Funktionen bestehen aus Polynomen im Zähler und Nenner.
Man unterscheidet zwischen echt und unecht gebrochen rationalen Funktionen.
Wichtige Eigenschaften sind Definitionslücken, Polstellen und Asymptoten.
Die Kurvendiskussion umfasst die Analyse dieser Eigenschaften zur genauen Bestimmung des Funktionsgraphen.